Codes available:
Pattern Detection
Higher Order Singular Value Decomposition (HOSVD)
HOSVD, or High Order Singular Value Decomposition, is a mathematical technique used in pattern detection and analysis for high-dimensional data. HOSVD can be used to decompose a high-dimensional tensor into a set of orthogonal rank-1 tensors, which represent the underlying patterns in the data. The technique allows for the extraction of features that are relevant for further analysis, such as the spatiotemporal behavior of a system.
HOSVD has been used in various fields, including image and signal processing, and has gained attention in fluid mechanics for pattern detection. By applying HOSVD to flow data, researchers can identify patterns related to vortices, turbulence, and other important fluid flow phenomena. HOSVD can also be used in combination with other techniques, such as machine learning algorithms or HODMD, to enhance the accuracy and predictive power of the analysis.

The following video explains how this algorithm is applied:
More details can be found in the book:
And application of the code in: Lazpita, E., Martínez-Sánchez, Á., Corrochano, A., Hoyas, S., Le Clainche, S., & Vinuesa, R. (2022). On the generation and destruction mechanisms of arch vortices in urban fluid flows. Physics of Fluids, 34(5).
Download the code for HOSVD in MATLAB version here, in Python version here, or open it in Colab.
Higher Order Dynamic Mode Decomposition (HODMD)
HODMD, or Higher Order Dynamic Mode Decomposition, is a mathematical technique used to analyze complex dynamical systems. It has gained attention in the fluid mechanics community as a powerful tool for pattern detection. HODMD enables the decomposition of high-dimensional data into a set of dynamic modes that represent spatiotemporal patterns in the data. These dynamic modes are computed by solving an optimization problem, which identifies the most relevant temporal and spatial patterns in the data. Once the dynamic modes have been computed, they can be used to perform a variety of analyses, including mode stability analysis, mode mixing analysis, and prediction of future behavior. By applying HODMD to flow data, researchers can identify patterns related to vortex shedding, boundary layer separation, and other important fluid flow phenomena.
HODMD is also applicable to other complex dynamical systems such as chemical reactions, biological processes, and weather patterns. Its ability to extract dynamic modes from high-dimensional datasets makes it a valuable tool for analyzing complex systems that are difficult to understand using traditional analysis techniques. The use of HODMD in combination with other methods, such as machine learning algorithms, can enhance the accuracy and predictive power of the analysis. As such, HODMD is an exciting and promising technique for pattern detection and analysis in a variety of fields, including fluid mechanics.

The following video explains how this algorithm is applied:
The following book details several applications of HODMD for pattern identification, temporal forecasting, data reconstruction, etc. The book also includes the Matlab codes and some test databases:
And the application of the code in: Lazpita, E., Martínez-Sánchez, Á., Corrochano, A., Hoyas, S., Le Clainche, S., & Vinuesa, R. (2022). On the generation and destruction mechanisms of arch vortices in urban fluid flows. Physics of Fluids, 34(5).
Download the code for standard HODMD in MATLAB version here, in Python version here, or open it in Colab.
Download the code for multi-dimensional iterative HODMD in MATLAB version here, in Python version here, or open it in Colab.
Low-cost Algorithms
Low-cost SVD
Low-cost singular value decomposition (LC-SVD) is a modal decomposition-based database reconstruction method used to enhance the resolution of optimally sampled experimental data using data assimilation. To achieve so, LC-SVD first uses pysensors, to identify the optimal sensor positions for a reduced (or available) number of sensors, ensuring that the most critical flow patterns are captured over time. The coordinates of these sensors are then used to collect experimental data optimally. Once the experimental data has been stored, LC-SVD is applied to enhance the resolution of the POD modes and temporal coefficients’ matrices, fusing the experimental database and its corresponding high-resolution numerical simulation. These reconstructed matrices are then used to reconstruct the high-resolution snapshots tensor. This novel method makes it possible to enhance the resolution of experimental data 50000 times its original size, 123 times faster than standard SVD, using 40% less memory, achieving in some cases reconstruction errors close to 0.5%.

Download the code for low-cost SVD in Python version here, or open it in Colab.
Low-cost HODMD
Large and complex datasets often present computational challenges, particularly when using standard Singular Value Decomposition (SVD). As dataset sizes grow, the scalability of conventional SVD becomes a major bottleneck, especially in applications requiring repeated computations.
To address this, Low-cost Higher Order Dynamic Mode Decomposition (lcHODMD) extends standard HODMD with a more efficient approach that reduces both memory usage and computational time. This method leverages either Low-cost Singular Value Decomposition (lcSVD) or Low-cost Higher Order Singular Value Decomposition (lcHOSVD) to enhance scalability and performance.
Reference us with:
ModelFLOWs (2023). ModelFLOWs-app. Retrieved [date], from https://modelflows.github.io/modelflowsapp/
Code in progress. Coming soon…
Spatial Resolution Enhancement
Gap Filling Tool
Gappy filling is a technique used to fill in missing or incomplete data points in a dataset, using various methods such as linear regression, interpolation, and extrapolation. The goal is to reconstruct a complete dataset that can be analyzed using traditional analysis techniques. The gappy filling tool aims to reconstruct the missing data points.

Application in complex databases:
Download the code for Gap Filling Tool in MATLAB version here, in Python version here, or open it in Colab.
Superresolution Tool
The super-resolution tool, based on SVD, is a technique used to improve the quality of a dataset that contains incomplete or noisy data. This technique involves using statistical methods to identify and remove noise from the data or to fill in missing data points with more accurate estimates. The goal is to produce a more accurate and reliable dataset that can be used for further analysis. The superresolution tool aims to improve the overall quality of the dataset.

Application in complex problems:
Download the code for Superresolution Tool in MATLAB version here, in Python version here, or open it in Colab.
Control
Passive Flow Control with HODMD
Based on HODMD, ModelFLOWs has been able to create a fully data-driven algorithm to calculate the so-called non-linear structural sensitivity. This concept identifies the region in the spatial domain where the flow is most prone to changes. Therefore, it has applications in flow control, as perturbing this region with a punctual force or a small geometric modification may delay the onset of some instabilities.
In linear theory, it is possible to calculate the structural sensitivity, but it is necessary to combine direct and adjoint solutions, as well as linearising the Navier-Stokes Equations. In realistic problems, these calculations would be expensive in terms of computational memory and time. Moreover, these algorithms cannot be applied to experiments or turbulent flows.
In the proposed method, any type of database (coming from experiments or numerical simulations) can be analyzed. The data-driven algorithm first filters the data in order to retain the most important dynamics. Then, the non-linear structural sensitivity can be calculated, using the DMD modes and the non-linear operator of the Navier-Stokes equations. A flow chart of the passive flow control process is shown below.
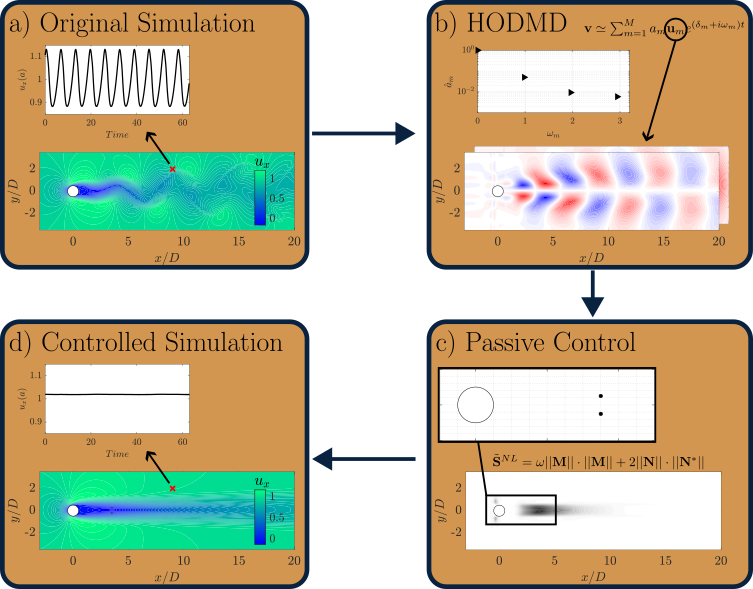
For a proper usage of the algorithm, it is recommended to first calibrate the HODMD algorithm, following the Advanced Tutorial in our website.
The following video explains how this algorithm is applied and the previous paper:
Download the code for Passive Flow Control with HODMD in MATLAB version here, in Python version here, or open it in Colab.
Passive Flow Control with Resolvent Analysis
This study introduces a data-driven flow control tool based on resolvent analysis, designed to identify the most sensitive regions of a flow field, areas where small perturbations can produce large effects. Using modal decomposition techniques and the HODMD algorithm, the method extracts coherent structures and quantifies the input–output gain that governs flow amplification mechanisms.
The approach enables the detection of regions of high structural sensitivity without requiring linearization of the Navier–Stokes equations or adjoint computations, making it suitable for complex or experimental data.
Two test cases are demonstrated:
- Flow past a circular cylinder, where the tool identifies optimal positions to introduce small stabilizing cylinders that delay vortex shedding and flow instabilities.
- Turbulent channel flow with heat transfer, where resolvent analysis highlights sensitive areas for geometric modifications (ribs and cavities). The resulting configurations achieve enhanced heat transfer (≈ +10%) while reducing drag (≈ –6%), outperforming conventional designs.
This algorithm provides a powerful, fully data-driven framework for passive flow control, applicable to laminar and turbulent regimes alike.
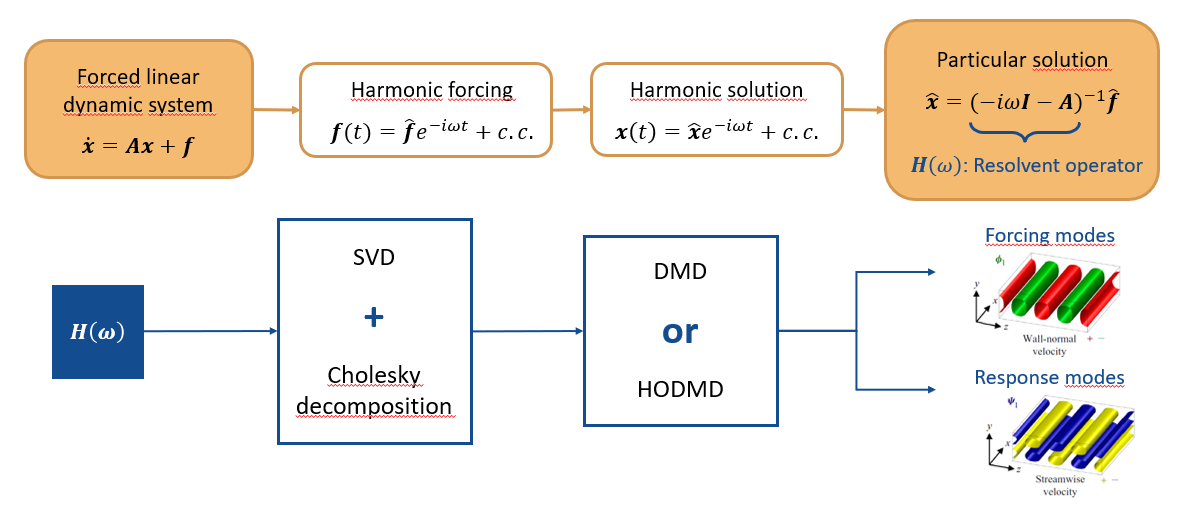
The following video explains how this algorithm is applied and the previous paper:
Download the code for Passive Flow Control with Resolvent Analysis in MATLAB version here, or the version including HODMD here.
For a proper usage of the algorithm, it is recommended to first calibrate the HODMD algorithm, following the Advanced Tutorial in our website.